Illustration
Pour produire des automobiles
nous avons besoin de main d'œuvre, d'une usine, de machines, de robots, d'énergie
et de consommations intermédiaires (tôles, moteurs, …) .
Que
nous produisions 1 seul véhicule ou bien 20 000 nous avons toujours besoin
d'une usine et des machines qu'elle contient, mais si nous produisons 20 000
véhicules plutôt qu'un seul nous aurons besoin de 20 000 fois plus de matières
premières.
L'usine
et les machines coûtent 5 millions d'euros, l'énergie, les consommations
intermédiaires, la main d'oeuvre nécessaire à la construction de chaque
véhicule coûtent 5 000 euros. Le constructeur vend chaque véhicule au prix
de 12 000 euros.
Application
1. Représenter la fonction de coût en faisant
apparaître les coûts fixes et les coûts variables.
C(x) = 5 000 000 + 5 000 x
Coût unitaire moyen : C(x)/x
2.
Démontrez la décroissance du coût unitaire moyen.
Pour
1 automobile, le coût de production est de 5 005
000 (5 000 000 + (5 000) 1)
Le coût unitaire moyen pour
la production d'une automobile est de 5 005 000/1 = 5 005 000 euros
Un
peu cher pour une voiture, même sans rajouter de marge.
Pour
2 automobiles, le coût de production est de 5 010 000 (5 000 000 + (5
000) 2)
Le
coût unitaire moyen pour la production de deux automobiles est de 5 010 000/2
= 2 505 000 euros
Cela
reste vraiment trop cher.
Pour
10 automobiles, le coût de production est de 5 050 000 (5 00 000 + (5
000) 10)
Le
coût unitaire moyen pour la production de dix automobiles est de 5 050 000/10
= 505 000 euros
Pour
500 automobiles, le coût de production est de 7 500 000 (5 000 000 + (5
000) 500)
Le
coût unitaire moyen pour la production de cinq cents automobiles est de 7
500 000/500 = 15 000 euros
Pour
2 000 automobiles, le coût de production est de 15 000 000 (5 000
000 + (5 000) 2 000)
Le
coût unitaire moyen pour la production de deux mille automobiles est
de 15 000 000/2 000 = 7 500 euros
Le
coût unitaire moyen est donc bien décroissant, nous en concluons que si l'on
dispose d'une chaîne de production d'automobiles dont le coût fixe est supposé
connu, plus le nombre de voitures fabriquées augmente, plus le coût moyen
unitaire diminue se rapprochant de plus en plus du coût marginal (soit 5 000
euros dans notre exemple)
3.
Supposons que chaque véhicule produit est vendu à 11
000 euros, déterminez graphiquement le niveau de production nécessaire
pour que l'usine soit rentable (le seuil de rentabilité).
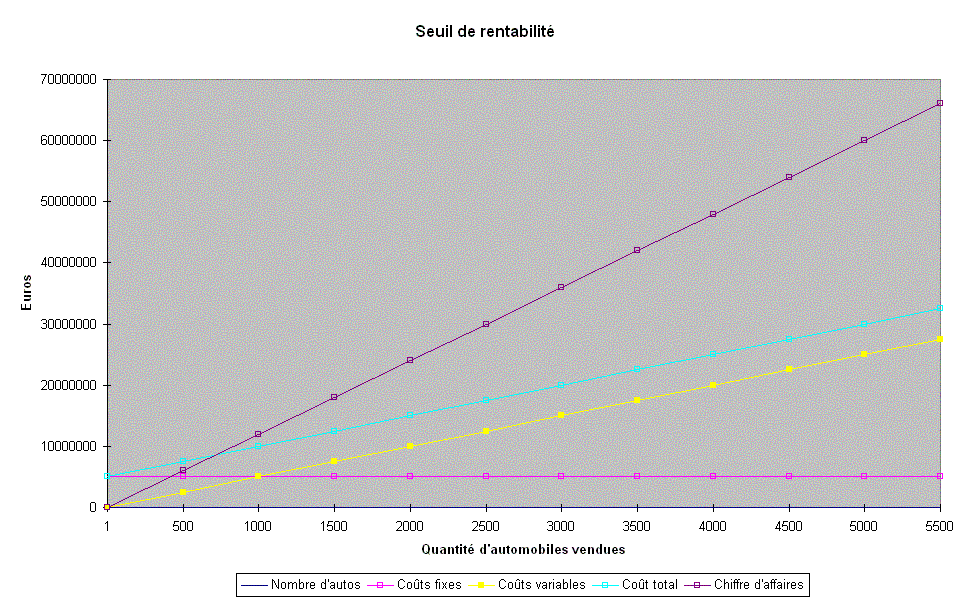
L'impact des coûts fixes est
plus ou moins important selon le type de production. Lorsque les coûts sont
élevés, la rentabilité est liée au dépassement d'un certain niveau de vente
que l'on appelle seuil
de rentabilité (ou point
mort). Le seuil de rentabilité est le chiffre d'affaire qui permet de couvrir
l'ensemble des frais de fonctionnement.
On le trouve graphiquement,
mais aussi mathématiquement : CA = C(x) Þ 11 000 x = 5 000 000 + 5 000 x Þ 6 000 x = 5 000 000 Þ x = 834.
Donc le point mort est atteint
au 834ème véhicule.
4.
La saboterie Philémon possède un atelier dont les coûts
fixes sont de 100 000 euros, ses coûts variables sont de 10 euros, elle
produit 600 paires de sabots au cours de la première année.
La saboterie Berule possède des coûts fixes de 50 000 et des
coûts variables de 10 euros, elle a atteint un capacité de production
de 1 200 paires de sabots par an et en est à la fn de sa deuxième
année d'exploitation. Calculer les coûts unitaires pour chacune
de ces entreprises.
Saboterie Philémon
: C(x) = 100 000 + 10 x ; donc C(x)/(x) = (100 000 + 10 x)/x ; pour la six-centième
paire de sabots le coût unitaire est de (100 000 + 6 000)/600 = 106
000/600 = 176,67 euros.
Saboterie
Berule : C(x) = 50 000 + 10 x ; donc C(x)/(x) = (50 000 + 10 x)/x ;
pour la deux-mille-quatre-centième paire de sabots le coût unitaire
est de (50 000 + 24 000)/2 400 = 74 000/2 400 = 30,84 euros.
5.
On suppose que 36 euros est le prix qui s'est établi sur le marché
des sabots haut de gamme, auquel correspond la production de ces entreprises.
Ces saboteries sont-elles rentables à ce prix ?
Oui
pour la saboterie Berule, non pour la saboterie Berule qui devrait produire
au moins 3 847 paires pour devenir rentable : (100 000 + 10 x)/x = 36 Þ 100 000 + 10 x = 36 x Þ 100 000 = 26 x Þ
x
= 3 847.
des coûts fixes, c'est à dire des coûts dont le montant ne varie pas
quelles que soient les quantités produites (du moins jusqu'à ce que l'on
ait atteint un taux d'utilisation des capacités productives de 100 %), il
s'agit en général des équipements, des machines, des
installations, on peut aussi y ajouter des coûts liés à
des investissements immatériels tels que le R&D, la formation,
la publicité ; 